Conservatoire national des arts et métiers
Architectures des systèmes informatiques
CHAPITRE 8
Complexité, Puissance et Variabilité
Année 2002-2003

Try to imagine studying physics without a measure of length other than «Object A looks larger than Object B» or studying chemistry without a measure of temperature better than «The reaction vessel became very hot». Without absolute metrics, sciences remain in a state of infancy. That is the state that computer science has been in.
        John Gustafson, Laboratoire Ames, département américain de l'énergie.
Essayez d'imaginer l'étude de la physique sans autre mesure de la longueur que «L'objet A semble plus long que l'objet B» ou l'étude de la chimie sans une mesure de la température meilleure que «Le réacteur est devenu très chaud». Sans métriques les sciences restent en enfance. C'est l'état de l'informatique.

8.0 INTRODUCTION

Nous utilisons ici les trois mots complexité, puissance et variabilité dans leur sens commun et non dans les sens savants qui seraient algorithmique pour le premier, physique pour le second et génétique pour le troisième.

• Complexité d'une chose qui a un nombre de composants ou d'états tels que l'on ne peut pas l'appréhender clairement dans sa totalité ou dans tous ses aspects.

• Puissance d'un appareil, capable de fournir un travail.

• Variabilité d'un phénomène ou d'une situation qui présente simultanément des aspects distincts à des observateurs différemment placés ou, en forçant le trait, autant d'aspects que de lieux d'observation.

Ce chapitre contient :
un aperçu sur la complexité d'un système informatique;
un examen de ce que l'on peut nommer puissance d'un système informatique et les évaluations que l'on fait des unités centrales;
quelques techniques d'évaluation des performances;
un aperçu de l'influence du logiciel sur les performances;
la conclusion du chapitre;
une note sur la variabilité.

8.1. LA COMPLEXITÉ D'UN SYSTÈME INFORMATIQUE

A distinguishing characteristic of computer science is the enormous gap that exists between the simple instruction sets of our computers and the complexity of useful software. This dichotomy produces intellectual challenges of the highest order. Today many important applications contains several million lines of code, too many for one person to read in a year and impossible for one person to fully understand. VLSI chips are now being manufactured containing more than one hundred million transistors, again posing an almost impossible problem for human comprehension.

                                                        John Savage, Professeur à l'université de Providence, 1996

Un caractère remarquable de l'informatique est le fossé immense qu'il y a entre la simplicité des jeux d'instructions et la complexité des logiciels ordinaires. Cet écart engendre des défis intellectuels de la plus haute nature. Aujourd'hui, beaucoup de logiciels importants contiennent plusieurs millions de lignes de code, beaucoup trop pour qu'un individu puisse seulement les lire en une année et impossibles à être vraiment compris par une personne. Les puces de circuits intégrés vont contenir plus de cent millions de transistors, elles poseront elles aussi un problème impossible pour la compréhension humaine.

John Savage compare l'état des logiciels à celui du jeu d'instructions, et s'étonne de leur écart. Cet écart n'est pas plus grand, mutatis mutandis que celui qu'il y a entre l'œuvre de Balzac et le lexiques des mots de sa langue. Il y a également un fossé considérable entre la simplicité des jeux d'instructions, surtout celui des machines RISC, et la complexité architecturale des processeurs que l'on a vue dans les chapitres précédents.

Cette complexité tient autant au nombre de composants qu'à la difficulté induite par leur organisation et par leur fonctionnement en l'absence de lois générales et de règles de construction ou d'agrégation.

Cette complexité a pour origine le nombre de composants et le nombre d'états distincts que le tout peut avoir.

• Le nombre de composants est grand : de quelques dizaines à des milliers de circuits intégrés et chacun d'entre eux contient de mille à plusieurs millions de composants dans des structures microscopiques.
• Le nombre d'états distincts est considérablement plus important puisqu'il procède de la combinatoire. Un banc de mémoire de 1 Mo a 2²³ points de mémoire ou bits (2²⁰ octets x 2³ bits/octet). À raison de 2 états pour chacun, il a 2^(2²³) états distincts, soit exactement 2 ^8*1000*1024 ou encore plus de 10^8000000 d'états. Ces nombres sont à comparer au nombre d'atomes de l'univers inférieur à 10⁸⁰ en l'état de nos connaissances; au temps écoulé depuis le «big bang» est d'environ 14 ou 15 milliards d'années. À raison de 365 jours par an, et 24 heures de 3600 secondes par jour, le nombre de secondes est de moins de 15*10^9*(1/3)*24*3600 ou encore moins de 10²⁰ microsecondes ou encore 10²³ nanosecondes. Nous aenviron 10⁹ neurones dans notre cerveau.

La complexité des algorithmes fait l'objet de très nombreuses études.
La complexité d'un programme ou d'un algorithme est abordée très brièvement plus loin.
La complexité d'un système informatique n'a pas fait l'objet de travaux aboutissant à des conclusions utilisables, à notre connaissance.

8.2 LA PUISSANCE D'UN SYSTÈME INFORMATIQUE

8.2.1 Puissance intrinsèque et puissance effective

Ici aussi, puissance a son sens banal : ce que «peut» faire la machine en cause; ce qu'elle contient en puissance avant de le manifester en actes. Cette puissance n'a aucun rapport avec la puissance définie en mécanique, en électricité et dans les autres domaines de la physique où l'on dispose de lois de conservation sous la forme d'équations de bilan avec leurs dimensions, leurs règles de composition et de calcul. Alors qu'il existe en mécanique des seuils minimaux pour vaincre un frottement ou la composante due à la pesanteur pour mouvoir une charge, il n'y a pas de tels seuils en informatique (sauf à avoir une alimentation électrique insuffisante). Ces points sont plus longuement développés dans la conclusion du cours.

Tout ordinateur, pourvu qu'il possède des caractéristiques minimales (n'importe quelle machine existante les a en surabondance) peut résoudre tout problème relevant de la classe des fonctions calculables. Mais la théorie, non seulement ne dit pas le temps nécessaire à leur exécution, mais n'aborde aucune considération de temps hors le fait de distinguer s'il est fini ou infini. Le temps nécessaire est fonction aussi bien de la complexité de l'algorithme de résolution du problème, du choix pertinent d'un langage et de son traducteur, de la qualité de l'expression sous la forme d'un programme, que des caractéristiques physiques architecturales et d'organisation de l'ordinateur d'exécution. C'est pourquoi nous sommes amenés à définir et à distinguer :

La PUISSANCE INTRINSÈQUE, c'est-à-dire la capacité à exécuter un algorithme. Elle est infinie au sens où tout algorithme bien conçu résolvant un problème calculable et bien exprimé dans un langage adéquat, sera exécuté sur n'importe quel ordinateur en un temps fini, pourvu que l'universelle capacité de celui-ci n'ait pas été masquée.

Les PUISSANCES EFFECTIVES, que l'on doit plutôt nommer PERFORMANCES relèvent des :

• temps de réponse (latency), ou temps d'exécution ou encore temps de latence. C'est le temps qui s'écoule entre le début et la fin d'un travail. Les deux premiers sont utilisés pour l'exécution d'un programme ou d'une tâche. Le temps de latence est appliqué à la mémoire et aux entrées et sorties. Ce temps de réponse intéresse l'utilisateur devant sa machine en mode interactif.
• débit (throughput) ou bande passante (bandwith). C'est la quantité de travail faite par unité de temps. Le débit est appliqué à l'exécution des programmes ou des tâches. La bande passante s'applique à la mémoire et parfois aux entrées et sorties. Ce débit intéresse le responsable de centre informatique.
• utilisation ou plutôt temps d'utilisation ou temps d'occupation ou taux d'occupation. C'est le temps ou la fraction de temps pendant lequel un composant ou un système est occupé.
• volume disponible que l'on oublie le plus souvent, c'est la capacité à enregistrer le volume des données.

• l'aptitude à traiter un seul problème posé ou encore rapidité d'un traitement. Elle sera grossièrement inverse du temps d'exécution, dépendra de la mémoire installée, de son utilisation, du processeur, du langage, de l'algorithme utilisé etc. Elle intéresse l'utilisateur qui attend le résultat;
• l'aptitude à traiter plusieurs problèmes en séquence ou en quasi simultanéité. Il s'agit ici d'un débit global. Il intéresse le gestionnaire d'une machine mise à disposition de plusieurs utilisateurs.

Une théorie achevée fonde la puissance intrinsèque parfaite et universelle. Elle ne peut apporter aucune lumière en matière de puissance effective.

C'est donc par des voies extérieures que doit être construit un discours et que doivent être établies des méthodes, des techniques, des procédés et des outils en matière d'architectures d'ordinateurs.

En ce domaine, tout va être accumulation d'inventions, d'expériences, de recettes et de tours de main avec deux conséquences ici aussi :

• un foisonnement des solutions architecturales sans qu'aucune ne s'impose réellement comme supérieure aux autres dans tous ses aspects;
• la nécessité de recourir, pour organiser la réflexion et l'étude, à des instruments extérieurs à la théorie. Le premier est le temps physique. Les autres sont de simples outils de classement comme des relations d'ordre, des grilles ou des repères.

• Le temps de réponse ou temps d'exécution ou temps de latence. C'est le temps écoulé entre le début et l'achèvement d'une tâche quelconque. On en a vu un exemple dans la caractérisation des mémoires.
• Le débit ou largeur de bande ou bande passante. C'est la nombre d'opérations (ou quantité de travail) faites par unité de temps. On en a vu un exemple dans la caractérisation des pipelines.

On peut définir deux mesures partielles :

• l'utilisation temporelle, temps pendant lequel le composant est occupé; elle est aussi exprimée en taux ou pourcentage d'un temps total;
• l'utilisation spatiale, quantité du composant qui est utilisée, elle est aussi exprimée en taux ou pourcentage de la quantité totale.

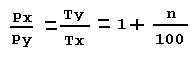
On doit dire alors en toute rigueur que Y est -n% plus rapide que X.

C'est une abus que de dire n% plus puissante au lieu de n% plus rapide.

8.2.2 De l'augmentation des performances ou la loi d'Amdahl

Pour augmenter la performance globale d'un système, il faut augmenter la performance d'un ou de plusieurs de ses composants.

Certains composants sont plus fréquemment utilisés que d'autres. Il paraît donc raisonnable de consacrer la dépense possible à améliorer les composants les plus utilisés plutôt que ceux qui le sont moins. Notons toutefois que la notion de composant le plus ou le moins utilisé dépend de la nature du travail. On l'a vu il y a très longtemps déjà quand dans les années 50, on a rendu simultanées les opérations d'entrées et sorties des machines consacrées à la gestion. À l'opposé, on n'achètera pas une machine pour le motif qu'elle a une unité de virgule flottante câblée, alors que les travaux à faire sont la comptabilité et la paye.

La loi d'Amdahl définit l'augmentation de la performance que l'on peut attendre d'une amélioration du système.

Utilisons les conventions suivantes :

.T est le temps d'exécution d'un programme sur le système d'origine.
.T_a est le temps d'exécution du même programme sur le système amélioré.
.f est la fraction du temps T concernée par l'amélioration.
.Ac est l'accélération obtenue par l'amélioration.

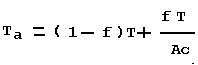
L'accélération obtenue est alors :

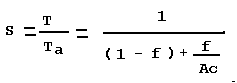
La loi d'Amdahl dit que la limite de l'accélération est :

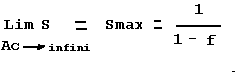
Exemple d'application :
Supposons que pour un programme rédigé en langage donné, le pourcentage du temps passé à faire du calcul vectoriel soit de 70%. Supposons de plus que la rédaction de cette partie en assembleur rende son exécution deux fois plus rapide, les calculs seraient les mêmes pour un câblage qui rendrait l'exécution deux fois plus rapide.

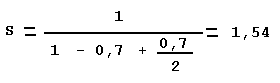
et à la limite :

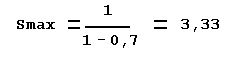
Introduction du coût

Considérons des systèmes S_i dont les coûts respectifs sont C_i.
Considérons des programmes P_j.
Considérons le temps d'exécution T_ji du programme P_j sur la machine S_i.
Le rapport coût à performance du programme P_j sur la machine S_i est

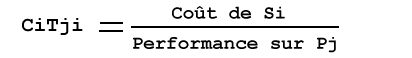
Une valeur plus grande de C_iT_ji signifie

• une moins grande performance à coût donné,
• un coût plus élevé à performance donnée.

8.2.3 Les évaluations des unités centrales

Les nombres de base sont relatifs :

• à l'unité centrale,

• au programme,

CPI = C/I et s'il y a partition :

CPI = {S(CPI_ixI_i)}/I = S (CPI_i x I_i/I), les sommes sont de i = 1 à n.

Le nombre de cycles pour le programme est alors :

• l'utilisation des cycles par programme et du temps de cycle T = CxT_h = C/F_h;
• en utilisant le nombre total d'instructions, le nombre de cycles par instruction et le temps de cycle, on écrit

qui montre l'importance de ces trois facteurs interdépendants sur lesquels on raisonne trop souvent séparément.

Avec la partition du jeu d'instructions, on écrit :

On ne peut pas modifier isolément CPI, I ou T_h,
T_h dépend au moins du matériel et de son organisation,
CPI dépend du jeu d'instructions, du matériel et du compilateur,
I dépend au moins du jeu d'instructions et du compilateur.
ATTENTION :
 
 

Ces évaluations ne valent que dans des conditions précises : programme unique; compilé avec un compilateur déterminé; processeur et système d'exploitation identifiés. Toute généralisation conduit à des conclusions fausses.

Exemple d'évaluation :

Dans une UC nommée A, le branchement se fait par le positionnement d'une condition en une instruction, le test et le branchement lui-même sont faits en une autre instruction. Le branchement demande ainsi deux cycles. Toutes les autres instructions demandent un cycle. Dans un programme 20% des instructions sont de tels branchements et 20% sont des placements de conditions. Le temps de cycle de A est 25% plus rapide que le temps de cycle d'une autre unité centrale nommée B qui fait le positionnement de la condition et le branchement en une seule instruction. Cette instruction demande deux cycles, toutes les autres se font en un cycle. Quelle est l'UC la plus rapide ?

Calculons :

CPI(A) = S CPI_ixI_i/I = 0,2x2 + 0,2x1 + 0,6x1 = 1,20

T(A) = 1,2xI(A)xT_h(A)

Comme l'unité centrale B ne demande pas de positionnement de condition, il y a 20 % d'instructions en moins, 25% (20/80) sont des branchements qui demandent 2 cycles.

CPI(B) = S CPI_ixI_i/I = 0,25x2 +0,75x1 = 1,25

T(B) = (0,8xI(A))x1,25x(1,25xTh(A))

Supposons que l'on puisse modifier le temps de cycle d'horloge de B, de combien faut-il le modifier pour que B et A aient la même performance dans ces conditions ? Soit X cette modification :

T(B) = (0,8xI(A))x1,25x(XxT_h(A)) or, on veut que T(A) = T(B)

donc 1,2 = 0,8x1,25xX et X = 1,2