Architectures des systèmes informatiques
CHAPITRE 8
Complexité, Puissance et Variabilité
Année 2002-2003
8.4 L'INFLUENCE DU LANGAGE DE PROGRAMMATION ET DES COMPILATEURS
On a rédigé avec le même soin quelques programmes en Bliss, langage de base de la série VAX, en Pascal et en C. On a observé leurs temps d'exécution sur le même Vax. Au plus la note est élevée, meilleure est la performance. La performance en C a été prise pour base.
| Programme | en Bliss | en C | en Pascal |
| Recherche | 1,24 | 1,0 | 0,70 |
| Crible | 0,63 | 1,0 | 0,80 |
| Puzzle | 0,77 | 1,0 | 0,73 |
| Ackermann | 1,20 | 1,0 | 0,80 |
La seule relation d'ordre observable est que Pascal est toujours moins efficace que C. Les dispersions de performances sont importantes. On en déduit que la part des compilateurs dans les temps d'exécution est importante.
Un compilateur
est aujourd'hui composé des parties suivantes :
.analyseur lexical;
.analyseur syntaxique;
.générateur de code
intermédiaire;
.optimiseur de haut niveau;
.optimiseur global;
.générateur de code
cible;
.arrangeur de code;
.éditeur de liens.
Les fonctions des parties relatives à l'optimisation sont les suivantes :
UN BANC D'ESSAI DE FOURNISSEUR DE COMPILATEURS
Alsys fournit des compilateurs ADA. Il utilise des programmes d'essais pour valider les performances et l'optimalité du code produit par un compilateur. Sous le nom de Bench, écrit bien sûr en ADA, ce banc d'essai contient :
|
|
n'a pas de signification scientifique car elle ne peut pas être mesurée. |
|
Il n'empêche que :
Les bancs d'essai peuvent être utilisés pour comparer deux machines entre elles. Celle qui a la meilleure note sera estimée la meilleure. Cette note est obtenue par calcul d'une moyenne, dont on connaît le peu de signification : si vous avez les pieds dans un congélateur et la tête dans un four, la moyenne dira que vous êtes bien. Il existe des moyens plus pertinents pour comparer des objets (mot pris dans un sens général) entre eux. Nous en présentons deux qui sont d'usage général.
Tout
d'abord, les objets à comparer doivent avoir des caractères
ou caractéristiques.
Des projets d'étude
auront un coût, une durée, une faisabilité, etc.
Des machines auront une
masse, un rendement, une puissance, etc.
Ces caractères doivent
évidemment être pertinents pour le but poursuivi. Il ne servirait
à rien de comparer la couleur d'appareils non visibles ni la consommation
électrique d'appareils mécaniques.
Ces caractères doivent
être appréciables sinon mesurables. Ces appréciations
vont du oui-non au repérage sur une échelle : de A à
E, de 0 à 10, de 0 à 100 etc.
Première méthode nommée Électre.
Elle date des années 1960. Elle a été inventée par Bernard Roy [ROY68] et appliquée à ses débuts par la SEMA (société d'électronique et de mathématiques appliquées) pour évaluer conjointement des projets de recherche. Des logiciels de mise en œuvre sont disponibles à l'université Dauphine [DAU00]. Nous n'en donnons qu'un très bref aperçu.
En usage manuel, la liste des caractères est portée sur un axe horizontal. Chaque point de l'axe porte une verticale graduée selon les appréciations possibles du caractère. Ensuite chaque projet est repéré par la ligne brisée qui joint ses points représentatifs.
Exemple
:
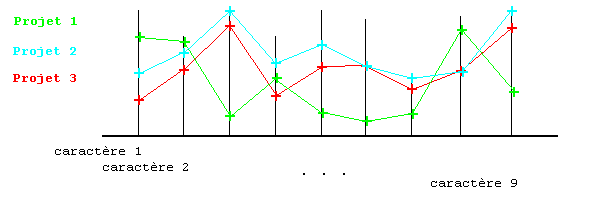
On observe :
.que le projet 2 surclasse
ou est égal au projet 3, 2 est meilleur que 3;
.que le projet 1 est tantôt
meilleur tantôt moins bon que chacun des deux autres.
Si l'on
doit choisir entre 1 et chacun des deux autres, on procédera en relevant
séparément les caractères pour lesquels 1 surclasse
un autre projet et les caractères où 1 est surclassé
par le même.
La nature des caractères
pourra être prise en compte pour chacun de ces deux relevés.
Exemple : si 1 surclasse
2 en termes de délai d'attente et si la politique choisie est le court
terme, 2 sera éliminé par rapport à 1.
Le fond de l'affaire consiste à comptabiliser séparément les avantages de 1 par rapport à 2 et les avantages de 2 par rapport à 1. Dans la réalité, il n'y a pas de compensation du mauvais par le bon. Nous ne sommes pas dans le cas d'école bien nommé, où une bonne note en compense une mauvaise. La moyenne arithmétique, géométrique ou harmonique n'est que très rarement pertinente.
Deuxième méthode, le graphe de Phil Kiviat.
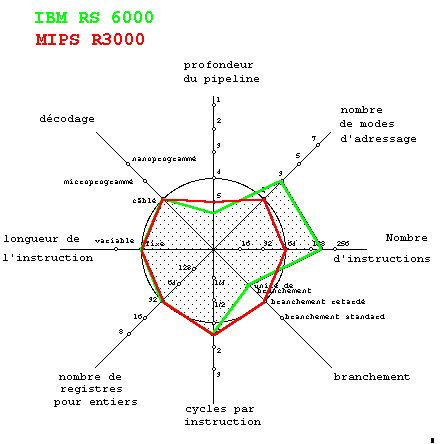
Elle date des années 1970. Elle a les mêmes prémisses que la précédente, sa présentation est différente. Au lieu d'aligner les caractères sur un axe, ils sont portés par des rayons issus d'un point. La suite de la démarche est libre.
L'exemple suivant est adapté de [ESP91]
On y
présente conjointement 8 caractéristiques censées être
pertinentes vis-à-vis de la nature RISC (vers le centre de la figure)
ou non-Risc (vers l'extérieur) d'un processeur. Les processeurs comparés
sont l'IBM RS6000 et le MIPS R3000.
8.7
NOTE COMPLÉMENTAIRE SUR DES MESURES DE COMPLEXITÉ DU LOGICIEL
Notons tout d'abord
les premières observations relatives aux répartitions des instructions
par importance relative. Daniel Knuth a observé en 1971 que «grossièrement 4% du volume d'un programme,
est cause de la moitié du temps d'exécution».
Les liaisons étroites et
l'indiscernabilité des composants matériels et logiciels selon
le point de vue adopté, conduisent à dire quelques mots de
la complexité du logiciel et des tentatives de mesure de cette complexité.
Le modèle de MacCabe
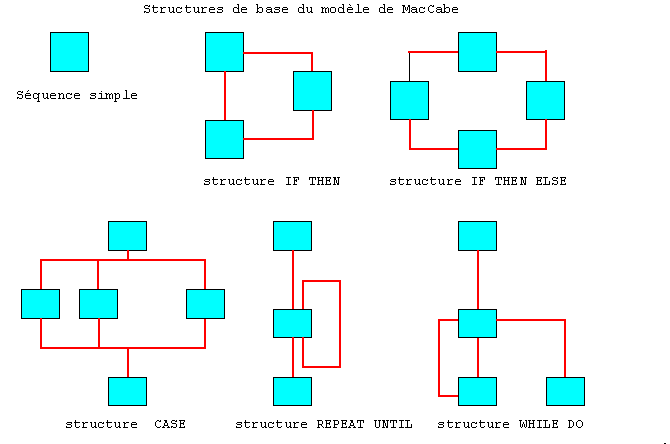
MacCabe [MCA76] a défini un modèle qui consiste à construire un graphe et à calculer un nombre sur lui.
1) Le graphe
Un bloc de base est une séquence
d'instructions sans branchement ni boucle. Il a un point d'entrée et
un point de sortie.
Pour un programme
P, on construit le graphe G(P)=[V,E] structure logique du programme, où
:
V ensemble des sommets représentant
chacun un bloc de base,
E ensemble des flèches qui
représentent la possibilité d'un transfert de contrôle
entre deux blocs de base.
On représente G par une matrice d'incidence A dont l'élément Aij=1 si un transfert de contrôle peut être fait du bloc i au bloc j, sinon Aij=0.

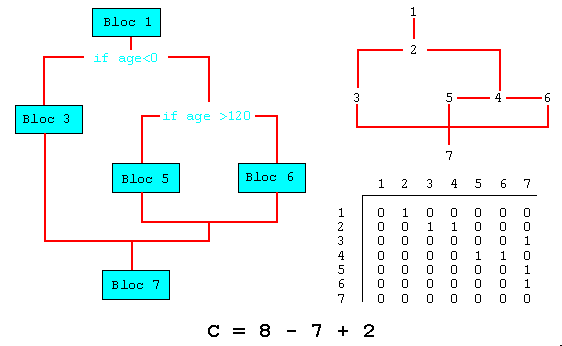
MacCabe a montré que C peut être calculé d'une autre façon, sans construire le graphe.
C est
la somme des éléments relevés comme suit :
a) +1 pour chaque instruction alternative
telle que IF, CASE et autres,
b) +1 pour chaque boucle ou construction
répétitive telle que DO DO-WHILE,
c) +N-2 pour un CASEn où N
est le nombre de possibilités,
d) +1 pour chaque opérateur
logique AND ou OU relevé dans un IF.
Des variantes
ont mené à définir trois nombres :
CYCMAX nombre cyclomatique en appliquant
les 4 règles précédentes, métrique de MacCabe;
CYCMID en appliquant a) b) et c),
métrique de Myers;
CYCMIN en appliquant a) et b) seulement,
métrique de Hansen.
Dans les cas réels, les valeurs de ces trois nombres sont toujours très fortement corrélées.
Le modèle de Halstead
Halstead a construit une complexité textuelle à partir de la théorie de l'information. Il calcule la quantité totale d'information contenue dans le programme. Pour cela, il fait un codage minimal du programme écrit. Il distingue deux classes seulement de symboles, les opérateurs qui sont les mots réservés du langage, et les opérandes définis par l'utilisateur, c'est-à-dire les noms de variables, de procédures, les chaînes de caractères etc. Les nombres d'opérateurs et d'opérandes rencontrés et leur nombre d'occurrences sont comptabilisés. On calcule ensuite le nombre minimal de bits nécessaires et suffisants pour coder ces deux types de symboles. Rappelons que si un vocabulaire est de taille N, chacun de ses éléments est codable avec log2(N) bits et que le nombre de bits nécessaires pour représenter p fois un de ces éléments est plog2(N).
La complexité du texte est mesurée par la quantité d'information de Halstead V du programme :
V = N*log2(n) = (N1 + N2)*log2(n1+n2)
où n1 est le nombre d'opérateurs
distincts et N1 le nombre de leurs occurrences,
où n2 est le nombre d'opérandes
distincts et N2 le nombre de leurs occurrences,
Dans le programme ci-dessus, on compte :
| Opérateurs | occurrences | Opérandes | occurrences |
| Program
; Var : integer Begin Write ( ) Readln If < Then writeln Else > End . |
4 1 1 1 1 1 4 4 1 2 1 2 3 2 1 1 1 |
VERIF_AGE
age 'Donnez...' 0 'Erreur...' 120 'Vous êtes...' 'Age enregistré' |
4 1 1 1 1 1 1 |
|
|
|
|
|
Par application de la formule :
V = (32+11)*log2(18+8) = 202,12
Remarquons que la distinction entre opérande et opérateur est ambiguë dans les langages à types.
Il bien d'autres modèles. Certains prennent en compte le nombre de niveaux engendrés, notion de complexité hiérarchique.
Elle ne vise pas la diversité des architectures d'ordinateurs différents mais les caractères propres à chacun d'eux.
Prenons comme objet d'étude un petit ordinateur; le lecteur se rendra compte aisément que les conclusions seraient les mêmes pour toute autre machine.
Le premier observable est la carte qui porte l'unité centrale : processeur, circuits d'entrée et sortie, canaux, mémoire, bus, commande des bus, etc. Elle est accompagnée de dispositifs accessoires cartes additionnelles, disques, etc.
L'ensemble peut être représenté par des schémas qui détaillent les composants fonctionnels indépendamment de leur implantation. C'est là une première description architecturale. Elle doit être complétée par la description électrique du fonctionnement des composants. Est-ce là l'architecture du système, même si on la complète par les disques, écrans, claviers, imprimantes, etc. ?
C'est l'architecture physique, celle du concepteur de la carte, celle que voit le réparateur de composants, mais cette carte n'est pas commandable en l'état, on ne peut pas lui appliquer des ordres exécutables. Elle est encore inutilisable.
Pour la programmer, un jeu d'instructions de base été prévu dans le processeur. Quel que soit leur nombre, ces instructions rendent accessible une partie très limitée de la machine. Des opérations plus compliquées que celles du jeu sont faisables par l'exécution successive de plusieurs instructions de base.
Ces instructions de base, exprimées sous la forme de mnémoniques, forment le langage d'assemblage et fournissent une description de l'atteignable, très différent du précédent pour la même machine.
Certains organes présents dans la première ne figurent pas dans la seconde, bascules, registres non accessibles, fils d'alimentation, commande de rafraîchissement de mémoire dynamique. Réciproquement dans les machines microprogrammables ou qui contiennent des dispositifs de nature voisine, des organes présents dans la seconde ne figurent pas dans la première.
|
|
ARCHITECTURE INDUITE PAR LE JEU D'INSTRUCTIONS |
|
| PILE | ACCUMULATEUR | REGISTRES |
| PUSH
A PUSH B ADD POP C |
LOAD
A ADD B STORE C |
LOAD
R1,A ADD R1,B STORE C,R1 |
Les représentants les plus exemplaires de ces architectures ont été :
Pile
: Burroughs 5500, Hewlett Packard 3000/70
Accumulateur : Digital Equipment
PDP 8, Motorola 6809 (microprocesseur)
Registres
: IBM 360, DEC VAX
Passons maintenant au delà de l'étape qui consisterait à examiner l'architecture ou les modifications induites par un système d'exploitation, ce qui constituerait une «visibilité» supplémentaire, et examinons ce que voit un programmeur s'exprimant dans un langage dit «évolué».
Les registres ont disparu, la mémoire également; apparaissent les chaînes de caractères, les numériques, entiers et autres, des structures différentes telles que POUR, JUSQU'À au lieu du test du passage à zéro de registres, SI----ALORS----SI NON au lieu du saut conditionnel sur valeur contenue dans un registre ou un indicateur, etc.
|
|
ARCHITECTURE INDUITE PAR LE LANGAGE D'APPLICATION. |
|
|
|
ARCHITECTURE INDUITE PAR LE LOGICIEL D'APPLICATION. |
|
Nous dirons donc :
|
|
Il a AUTANT D'ARCHITECTURES QU'IL Y A DE VISIONS POSSIBLES du système en cause. |
|
Ceci explique la variabilité annoncée début de ce chapitre et justifie la nécessité de la prendre en charge. Nous avons essayé de construire une filiation entre la théorie fondatrice et les architectures et nous avons vu qu'il n'y en a pas, sauf celle qui associe la machine à accumulateur aux fonctions calculables et la machine à pile aux fonctions récursives. Mais cela ne veut pas dire que l'on ne peut pas déduire des structures à partir de prémisses différentes. Deux voies sont possibles :
Cas particulier des machines-langage :
Il existe pour elles un moyen de principe. Il repose sur une définition préalable de la classe de problèmes à résoudre. Cette classe étant cernée au mieux, la deuxième étape consiste à la spécifier avec le plus de rigueur possible par un langage représentatif des moyens propres à résoudre ces problèmes. Ce langage doit, bien entendu, être formel.
Une façon simple de définir un langage consiste à écrire son automate de reconnaissance, c'est-à-dire les règles à appliquer pour décider si une phrase appartient ou non à ce langage. Le praticien dira alors que cet automate est le processeur du langage une fois qu'il sera réalisé en fonction des possibilités techniques du moment,.
C'est la définition de principe de ce que l'on appelle les «machines langage» quine sont pas des vues de l'esprit. On a mentionné au début de la première partie que Burroughs a construit la B1700 qui était une machine «nimporte quel langage» par microprogrammation . Plus récemment, la Pascaline était une machine-Pascal dans les années 80, Lilith de N. Wirth était une machine-Modula, on a évoqué des processeurs Java.
La réalisation
des machines-langage.
On perçoit assez clairement
l'apport majeur de la puissance intrinsèque. En effet, puisqu'une machine
de Neumann est universelle et qu'il ne peut être question de traiter
des fonctions non calculables, il suffira de simuler ou émuler la
machine-langage sur une machine conventionnelle, sans même avoir besoin
de fabriquer le processeur spécialisé. Cette simulation pourra
être faite aussi bien par un programme somme toute banal qu'en microprogrammant
la nouvelle machine si elle le permet. On qualifie aussi ces machines de
dédiées. Ce qualificatif, mauvaise traduction mot pour mot
de l'américain «dedicated», est pris dans le sens où
elles ont reçu une spécialisation sans obligatoirement en détruire
l'universalité.
Conservatoire national des arts et métiers
Architectures des systèmes informatiques
CHAPITRE 8
Complexité, Puissance et Variabilité
Année 2002-2003
![]()
![]()